16進数ってなに? 役に立つかもしれない知識
16進数値?覚えなくてもいいけどわかると楽しい
16進数値はHTMLではRGB値、ネットワークではIPアドレス、といったようにところどころで利用される数値です。HTMLやCSSを記述する上で重要ではないので、必要ない方は飛ばしてください。
進数とは
私たちが一般的に利用している数値は10進数といって0-9までの数字を利用しています。進数は進む数と書きます。なにが進むかというと桁が進む(増える)数を表しており、10になると桁が進む、つまり2桁になるということです。
進数の代表的なものには2進数、8進数、16進数があり、それぞれ桁が変わるタイミングが異なります。
2進数では2で桁が進むため、2という数字は使いません。0、1、2←ここで桁が進むため、10が2と同じ数値となります。
8進数では0、1、省略、7、8←ここで桁が進む(8は使わない)ため、10が8と同じ数値となります。
16進数では0、1、省略、8、9の次は桁は進まずアルファベットを利用し、10の代わりにa、11の代わりにb、12の代わりにc、13の代わりにd、14の代わりにe、15の代わりにf、次のg←ここで桁が進む(gは使わない)ため、10が16と同じ数値となります。
| 進数 | 進み方()内は10進数での表記 | |||||
|---|---|---|---|---|---|---|
| 2進数 | 0 (0) | 1 (1) | 10 (2) | 11 (3) | 100 (4) | 101 (5) |
| 110 (6) | 111 (7) | 1000 (8) | 1001 (9) | 1010 (10) | 1011 (11) | |
| 8進数 | 0 (0) | 1 (1) | 2 (2) | 3 (3) | 4 (4) | 5 (5) |
| 6 (6) | 7 (7) | 10 (8) | 11 (9) | 12 (10) | 13 (11) | |
| 14 (12) | 15 (13) | 16 (14) | 17 (15) | 20 (16) | 21 (17) | |
| 16進数 | 0 (0) | 1 (1) | 2 (2) | 3 (3) | 4 (4) | 5 (5) |
| 6 (6) | 7 (7) | 8 (8) | 9 (9) | a (10) | b (11) | |
| c (12) | d (13) | e (14) | f (15) | 10 (16) | 11 (17) | |
| 12 (18) | 13 (19) | 14 (20) | 15 (21) | 16 (22) | 17 (23) | |
| 18 (24) | 19 (25) | 1a (26) | 1b (27) | 1c (28) | 1d (29) | |
| 1e (30) | 1f (31) | 20 (32) | 21 (33) | 22 (34) | 23 (35) | |
2進数や16進数を10進数に変換
私たちが一般的に利用している数値は10進数の数字は以下のようにして成り立っています。10進数では10で桁が上がり10の位となり、次の桁は100の位と表現します。
2進数、8進数、16進数の数字を、10進数を元に位で表すと、以下のようになります。例えば2進数では2で桁が上がり2の位、次は4で桁上がり4の位、となります。
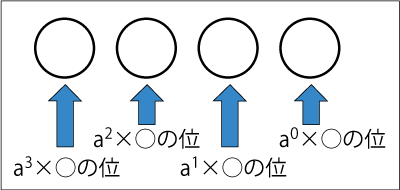
上の数値には規則性があり、以下のように説明できます。
a進数の桁が上がるごとに、「aを桁数から1引いた数をかけた(累乗)した数字」と「各桁の数字」を掛けた数字が各桁の10進数の数値なので、その数値を全て足すと10進数に変換できます。(1桁目は0乗、2桁目は1乗、3桁目は2乗、、、)
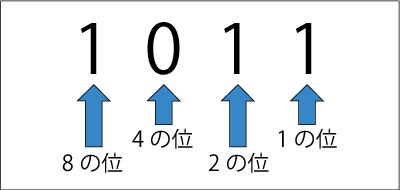
2進数での1011という数字の場合、
1桁目は1で、aは進数=2となり
2011が2進数で表記されている場合、
n桁目が○で、aをn-1乗した数と○を掛け算した数が各桁の10進数です。
1桁目が1で、2を1-1乗(つまり2の0乗=1)した数と1を掛け算します。→1
2桁目が1で、2を2-1乗(つまり2の1乗)した数と1を掛け算します。→2
3桁目が0で、2を3-1乗(つまり2の2乗)した数と0を掛け算します。→0
4桁目が1で、2を4-1乗(つまり2の3乗)した数と1を掛け算します。→8
上の各桁の数値を全て足し算(1+2+0+8)した結果の11が10進数に変換した数値です。
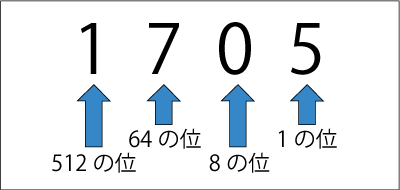
1705が8進数で表記されている場合、
n桁目が○で、aをn-1乗した数と○を掛け算した数が各桁の10進数です。
1桁目が5で、8を1-1乗(つまり8の0乗=1)した数と5を掛け算します。→5
2桁目が0で、8を2-1乗(つまり8の1乗)した数と0を掛け算します。→0
3桁目が7で、8を3-1乗(つまり8の2乗)した数と7を掛け算します。→448
4桁目が1で、8を4-1乗(つまり8の3乗)した数と1を掛け算します。→512
上の各桁の数値を全て足し算(5+0+448+512)した結果の965が10進数に変換した数値です。
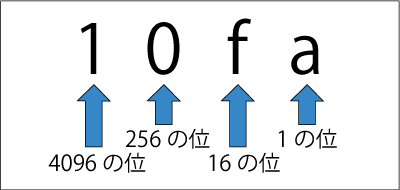
10faが16進数で表記されている場合、
n桁目が○で、aをn-1乗した数と○を掛け算した数が各桁の10進数です。
1桁目がaで、16を1-1乗(つまり16の0乗=1)した数とa(10)を掛け算します。→10
2桁目がfで、16を2-1乗(つまり16の1乗)した数とf(15)を掛け算します。→240
3桁目が0で、16を3-1乗(つまり16の2乗)した数と0を掛け算します。→0
4桁目が1で、16を4-1乗(つまり16の3乗)した数と1を掛け算します。→4096
上の各桁の数値を全て足し算(10+240+0+4096)した結果の4346が10進数に変換した数値です。
練習
10進数の35を2進数、8進数、16進数で表すとどのようになるでしょう。
2進数: 8進数: 16進数:
結果が表示されます